数据结构与算法
时间空间复杂度
算法是用来操作数据、解决问题的一组方法。主要是用事后统计法和事前分析估算衡量算法之间的优劣。 事后统计是通过统计、监控、利用计时器对不同算法的运行时间进行比较,从而确定算法效率的高低,但是有非常大的局限性。 事前分析估算是在计算机程序编写之前,依据统计方法对算法进行估算 比如斐波那契数列 0,1,1,2,3,5,7,13,求第 n 个斐波那契数
// 递归实现
function fun1(n) {
if (n <= 1) return n;
return fun1(n - 1) + fun1(n - 2);
}
// 循环实现
function fun2() {
if (n <= 1) return n;
let first = 0;
let second = 1;
for (let i = 0; i < n - 1; i++) {
let sum = first + second;
first = second;
second = sum;
}
return second;
}时间复杂度即运行消耗的时间,空间复杂度即消耗的内存空间 我们在计算时间复杂度时,代码每运行一次,记作一个单位时间,for(let i=0;i<n;i++)循环就是 n 个单位时间,以此类推计算出某个函数或者某个循环的时间复杂度 T(n)=O(f(n))公式
- T(n)表示代码执行的时间
- n 表示数据规模大小
- f(n)表示每行代码执行的次数总和
- 因为这时一个公式,所以用 f(n)表示。公式中的 O,表示代码的执行时间 T(n)与 f(n)表达式成正比,代表的是一种增长趋势
大数据规模时可以忽略掉“常数、低阶次、系数”都可省略,主要是找出对趋势起决定性作用的那个部分。 **大 O 时间复杂度实际上并不是具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以也叫做渐进时间复杂度,简称时间复杂度 ** n2 及以上阶的时间复杂度效率很低,递归的时间复杂度约为 2n,呈指数级,因此效率很低
时间复杂度还可分为最好情况、平均情况和最坏情况。  还可以考虑概率,但实际应用中,我们一般只看最坏的情况。
还可以考虑概率,但实际应用中,我们一般只看最坏的情况。
数组
数组下标都是从 0 开始,内存空间的地址是连续的
为什么很多语言中数组都从 0 开始编号
如何实现随机访问
数组是一种线性表数据结构,是一组连续的内存空间,存储具有相同类型的数据
关键词解析
线性表。排成线的结构,每个线性表上的数据最多只有前和后两个方向。除了数组,链表、队列、栈也是线性表结构 非线性表。二叉树、堆、图。因为这些数据类型不是简单的前后关系 连续的内存空间和相同类型的数据。数组正是因为如此,才得以有了随机访问的特性,但是对于数据的删除和插入,数组就显得有些低效,为了保证连续性需要做大量的搬移工作
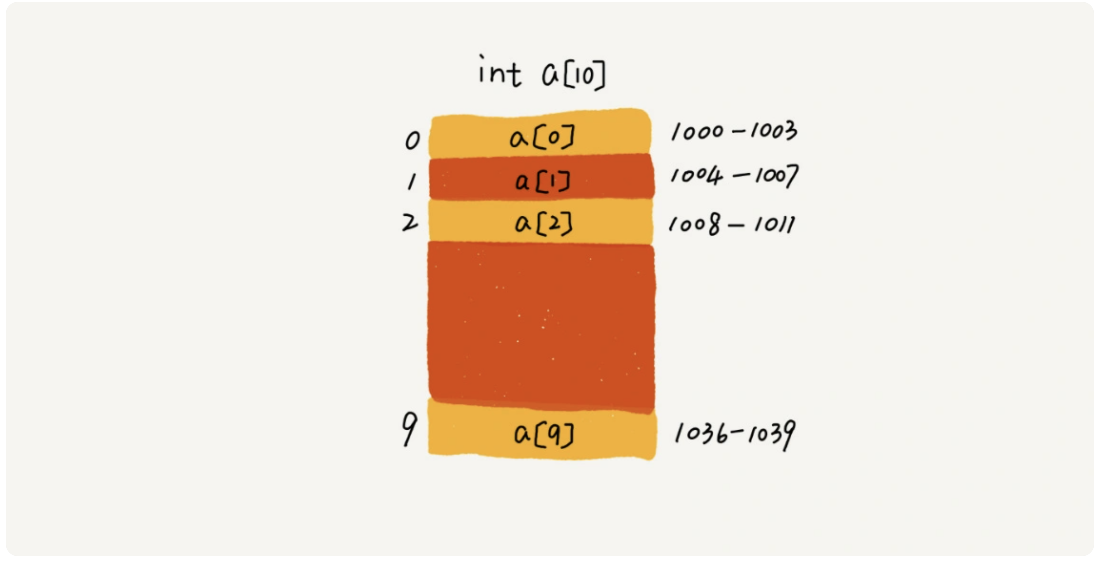
如图,一个长度为 10 的数组,计算机给数组分配了一块连续内存空间 1000-1039
首地址 base_address=1000
计算机会给每个内存单元分配一个地址,寻址公式a[i]_address=base_address+i*data_type_size
data_type_size表示数组中每个元素大小,通过首地址+下标乘以元素大小取到内存地址
数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)
为何数组的插入和删除操作是低效的
在中间插入元素,后面的都要移动,仅在末尾插入不需移动,平均时间复杂度为(1+2+...n)/n=O(n)
但如果不需要保持数组的有序性,直接插入到最后一个位置就可以了
要优化可以将多次的删除、插入操作集中在一起执行,这样元素尽量被少移动,大大减少了数据搬移的消耗
容器能否代替数组
不能
比如 java 的 ArrayList、C++ STL 中的 vector
使用容器的好处在于,将很多数组操作的细节封装了起来,比如数组插入、删除时搬移其他数据时。还有个优势是支持动态扩容。
数组需要预先指定大小,因为需要分配连续的内存空胶囊,比如我们只申请了 10,但是要用 11 时,我们需要重新分配一块更大的空间,将原来的数据复制过去,然后将新的数据插入
而 ArrayList 会在存储空间不够时,自动将空间扩容为 1.5 倍大小
数组的适用场景
- java 的 ArrayList 无法存储基本类型,int、long,需要封装为 Integer、Long 类,但是自动装箱、自动拆箱有一定的性能消耗
- 数据大小事先已知,操作简单
- 定义类型的时候更加容易。多维数组的类型声明可能会需要嵌套的泛型
解答:数组下标从 0 开始
- 数组下标的确切定义是偏移(offset),如果从 1 开始计数,每次还得(k-1)*type_size,从 1 开始编号,多了一次不必要的操作,数组作为基础数据结构需要高性能,所以从 0 开始
- 历史原因。C 是从 0 开始,java 等等都沿用
链表
链表与数组的差别在于,数组需要连续的存储空间,这就会导致如果所需的连续空降过大,会导致内存申请失败,即便总的多余内存时足够的,这时候,链表就更合适,因为链表不需要连续的存储空间,它可以将一组零散的内存块串联起来使用
链表常见的有三种
- 单链表
- 双向链表
- 循环链表
每个链表的节点除了存储数据之外,还需要记录链表上下一个节点的地址,这个地址叫做后继指针 next
只有头节点和尾节点是特殊的,头节点记录链表的基地址,尾节点指向一个空地址 null
链表同样支持数据的插入、删除、查找,在链表中进行插入、删除操作是非常快速的,因为不需要大量的数据搬移操作,但是数组由于不连续,没法随机访问,只能一个一个遍历节点,时间复杂度 O(n)
循环链表
循环链表是一种特殊的单链表,尾节点指针指向头节点
双向链表
每个节点有前驱后继两个指针,比单向链表需要更多的内存空间,更加好找前驱节点
链表的删除
链表的删除有两种情况
- 删除节点中某个值等于给定值的节点
- 删除给定指针指向的节点
第一种情况,单向链表和双向链表都需要依次遍历每个节点,O(n)
第二种情况,明显双向链表更好用,因为删除某个节点需要知道前驱节点,单链表又得遍历查找一遍
另外还有对于一个有序链表按值查找,我们可以按值决定往前还是往后查找,每次查找只需要查找一半的数据
实际使用中,双向链表也是更加广泛的,当内存空间充足的时候,追求代码的执行速度,双向链表是更好的,这也是空间换时间的思路。但如果内存吃紧,那就得采取时间换空间的思路
双向链表和循环链表还可以组合成双向循环链表
链表 VS 数组
数组简单易用,连续内存空间可以借助 CPU 的缓存机制,预读数组中的数据,而链表不是连续存储,CPU 缓存不友好
数组的缺点大小固定,连续的存储空间不够会导致内存不足,即便是内存足够,数组的扩容是需要把原数组拷贝一份的,这个操作相当费时,而链表本身没有大小限制,天然支持动态扩容,这是它与数组最大的区别
当然链表也比数组更加耗费内存,先不说前驱后继指针导致的内存空间翻倍,频繁的插入和删除操作,会导致内存的频繁申请和释放,容易造成内存碎片,高级语言会导致频繁的垃圾回收,所以对于数组和链表的使用,需要自己权衡场景
LRU 缓存淘汰算法
思路:维护一个有序单链表,越靠近尾部的节点是越早之前访问的,当有一个新的数据被访问时,我们从链表头开始顺序遍历链表
- 如果此数据已在链表中,我们遍历得到它后,删除,插入到头部
- 如果没在链表中,如果缓存未满,插入头部,如果缓存已满,删除尾节点,将新数据插入头部
此时总是需要遍历的,时间复杂度 O(n)
优化可以用散列表,可以降到 O(1)
注意事项
- 理解指针或者引用的含义。C 语言有指针,Java 没有,叫做引用,其实都是一样的意思,存储的是所指内存对象的内存地址。变量赋值给指针,其实是把变量的地址赋值给指针,指针或者引用指向这个变量,通过指针可以找到这个变量
- 警惕指针丢失和内存泄露。不需要的引用要及时断掉,引用也不要指错对象
- 使用哨兵简化实现难度。不管链表是不是空,head 指针一直指向哨兵节点,有哨兵节点的链表叫做带头链表。其实就是加了一个头节点,返回时候返回头节点的 next 就可以
- 留意边界条件处理。链表为空?链表只有一个节点?链表只包含两个节点?代码逻辑能否处理头节点和尾节点?
- 画图举例。光想容易不清晰,画出来更容易
- 多练习,没有捷径
栈
栈是一种操作受限的线性表,只允许一端插入和删除数据。从功能上来说,数组和链表都可以代替栈,但是操作的接口太多了。对于某些场景,需要这种约束事情才会变得更加可控
使用数组实现叫做顺序栈,使用链表叫做链式栈。入栈和出栈的空间复杂度是 O(1),时间复杂度也是 O(1)
出栈不涉及内存的重新申请和数据搬移,但是入栈的时候,如果空间不够,就需要重新申请内存和数据搬移,时间复杂度为 O(n)
栈在函数调用中的应用
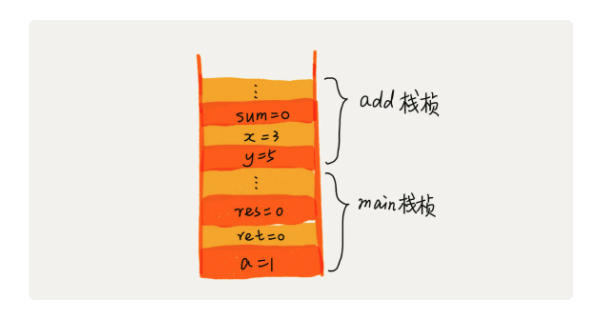
操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成栈这种结构,用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,函数执行完就弹栈
栈在表达式求值中的应用
求 34+13\*9+44-12/3 的值
编译器会通过两个栈,从左到右遍历表达式,遇到数字就压入操作数栈,遇到运算符,就与运算符栈的栈顶元素进行比较,优先级高的压入栈,优先级低或者相同的,从栈顶取出操作符和两个操作数进行计算,以此类推
栈在括号匹配中的应用
如何检查表达式中括号使用的合法性?
可以用栈保存未匹配的左括号,从左到右依次扫描字符串,左括号压入栈中,遇到右括号,从栈顶取出一个左括号,如果匹配,则扫描剩下的字符串,如果右括号不能配对,或者栈中没有数据,说明格式非法
队列
先进先出,入队出队,不允许其他操作,也是一种操作受限的线性表结构
有循环队列、阻塞队列、并发队列
实现队列可以用数组也可以用栈,分别叫顺序队列、链式队列
底层语言的数组在实现队列时,会导致头、尾下标的持续变化,所以需要在入队时,没有空间的情况下集中进行一次数据搬移的操作,另外,用循环队列可以更好地解决这个问题,循环的入队就可以了
阻塞队列和并发队列
阻塞队列
队列为空,从队列头取数据会被阻塞,因为没有数据可取,队列已满,插入数据会被阻塞。
这就是生产者——消费者模型的定义
并发队列
线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作。实际上,基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。在实战篇讲 Disruptor 的时候,我会再详细讲并发队列的应用。
线程池没有空闲线程时,新的任务请求如何处理?
- 非阻塞,直接拒绝任务请求
- 阻塞,请求排队,等到有空闲线程时取出排队的请求继续处理
基于链表和数组的队列对于排队请求有什么区别?
链表支持无限排队的无界队列,可能会导致过多请求排队等待,等待时间长
数组队列大小有限,当线程池中排队的请求超过队列大小时,接下来的请求会被拒绝,对空间响应时间敏感的系统来说,更加合理
对于大部分资源有限的场景,当没有空闲资源时,基本都可以通过队列的数据结构来实现请求排队
递归
递归需要满足三个条件
- 一个问题的解可以分解为几个子问题的解。比如电影院找座位,想知道自己的座位可以分解为前一排的人在哪一排的子问题
- 这个问题与分解之后的子问题,除了数据规模不同,求解的思路完全一样
- 存在递归终止条件
需要会写递归公式
写递归要注意避免堆栈溢出,可以通过限制递归调用的最大深度,超过该深度直接报错。但这种办法没有完全解决问题,仅在最大深度比较小的时候使用,比如 10、50。
还要警惕重复计算,可以使用散列表来保存已经求解过 f(k),当递归调用到时,先看下是否已经求解过了,是的话直接从三列表中取值返回,不需要重复计算
递归的空间复杂度是 O(n),因为每调用一次函数都会在内存栈中保存一次数据
递归有利有弊。它的表达力很强,写起来很简洁,弊端在于空间复杂度高,有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题,实际开发中,要根据实际情况来选择是否用递归的形式来实现
可以将递归改为迭代循环的非递归写法,但其实本质没有变,对于某些问题?还是无法避免
递归中还可能出现存在环形链表的问题,可以用快慢指针检测出环形链表的存在
排序
为什么插入排序比冒泡排序更受欢迎
排序算法的执行效率分析
- 最好、最坏情况、平均情况时间复杂度
- 时间复杂度的系数、常数、低阶。虽然一般情况下都可忽略,但是由于我们平时处理的数据可能规模不大,这个时候需要把这些考虑进去
- 比较次数和交换次数。基于比较的排序算法的执行过程,涉及元素大小的比较、元素的交换或移动,应该把比较次数和交换次数也考虑进去
排序算法的内存消耗
算法有空间复杂度,空间复杂度为 O(1)的排序算法叫做原地排序
排序算法的稳定性
待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变,叫做稳定的排序算法,否则叫做不稳定的排序算法
冒泡排序
每次对相邻的两个元素进行比较交换。可以优化当某次冒泡没有数据交换时,不再执行后续的冒泡操作
分析
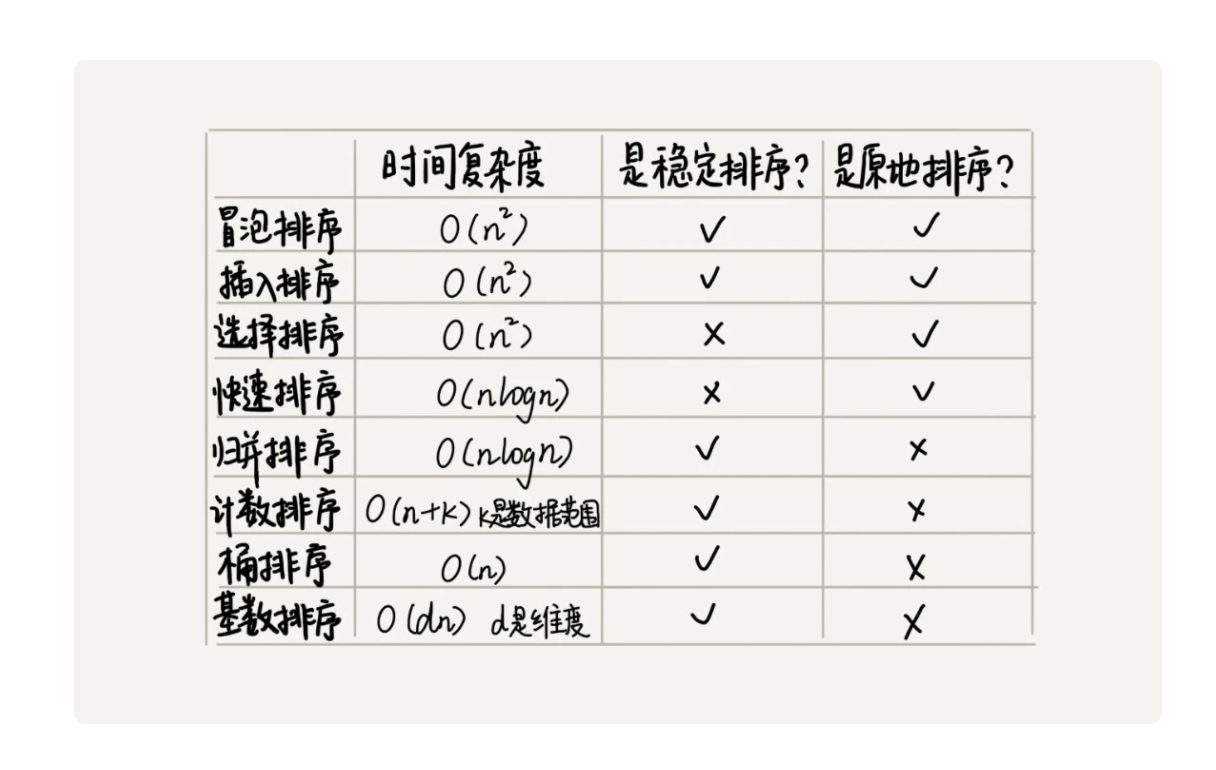
- 冒泡排序是原地排序算法
- 是稳定的排序算法
- 最好情况时间复杂度 O(n),最坏情况,当排序数据都是倒序排列的,需要 n 次冒泡操作,最坏情况时间复杂度 O(n^2)
对于包含 n 个数据的数据,排列方式不同,冒泡排序的执行时间也是不同的,可以用有序度、逆序度来分析
2,4,3,1,5,6 的有序元素有 11 对,如(2,4),(2,5),有序度 11,完全有序的数组,有序度是 n*(n-1)/2,叫做满有序度
逆序度以此类推,逆序度=满有序度-有序度
插入排序
将数据分为两个区间,已排序区间和未排序区间,核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入
不同的查插入点方法,元素的比较次数是有区别的,但对于一个给定的初始序列,移动操作的次数总是固定的,等于逆序度
分析
- 插入排序是一个原地排序算法,因为不需要额外的存储空间,空间复杂度是 O(1)
- 插入排序中,对于值相同的元素,可以选择将后面出现的元素插入到前面出现的元素的后面,所以是稳定的排序算法
- 如果原本已经有序,复杂度为 O(n),如果是倒叙,最坏情况时间复杂度是 O(n^2),平均时间复杂度为 O(n^2)
选择排序
从未排序的区间中找最小的元素,与已排序的元素的末尾+1 的元素进行交换
基本跟插入排序类似
分析
- 是原地排序算法
- 不稳定。因为每次都要交换元素位置
冒泡和插入排序在时间复杂度上是一样的,但冒泡排序涉及了 K 次交换操作,每次三个赋值语句,总耗时 3*K,插入排序数据移动操作只需要 K 个单位时间,性能上插入排序是更好的
归并排序
排序一个数组,先把数组从中间分成前后两部分,再对前后两部分分别排序,递归的形式,最终整个数组就排好序了
是分治思想的体现
分析
- 是稳定的排序算法。合并过程中可以保证值相同的元素,合并前后的顺序不变
- 时间复杂度 O(nlogn),归并算法的执行效率与要排序的原始数组的有序程度无关,时间复杂度很稳定,都是 O(nlogn)
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
......- 不是原地排序算法,空间复杂度 O(n)
快速排序
也是利用分治思想。选择一组数据中任意一个数据作为哨兵 pivot,遍历数据,将大于 pivot 的放到右边,小于 pivot 的放到左边,pivot 在中间,我们得到三部分的数据
我们可以递归哨兵左右的数据,直至区间缩小为 1,这样数据就有序了
递推公式:
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)
终止条件:
p >= r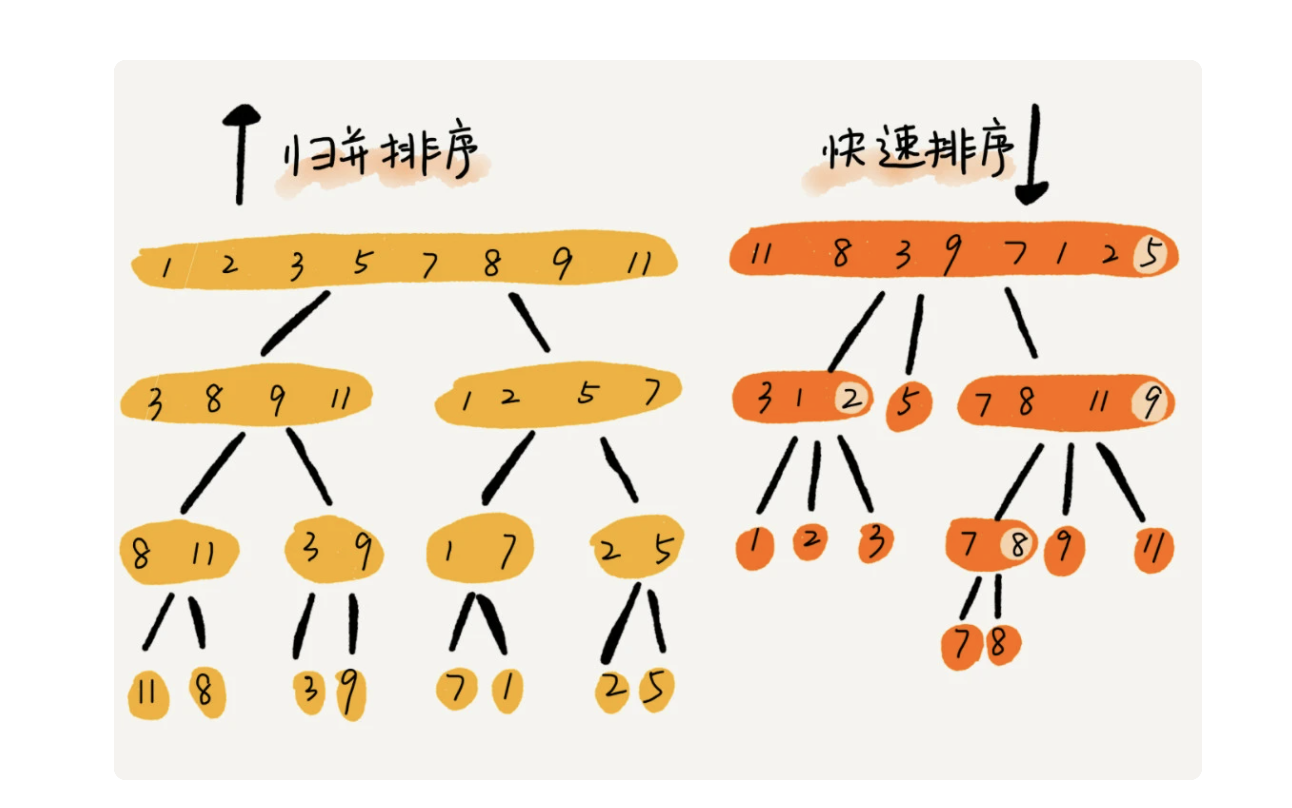
快速排序与归并排序的差别在于归并的处理过程由下到上,先处理子问题再合并,快排相反,从上到下,先分区,再处理子问题,归并虽然稳定、时间复杂度为 O(nlogn),但是是非原地算法。而快速排序通过巧妙的原地分区函数,实现原地排序,解决了归并排序占用太多内存的问题
分析
- 快速排序是一种原地、不稳定的排序算法。如果每次分区都能整好把数组分成大小接近相等的两个小区间,那么快排的时间复杂度递推求解公式跟归并是相同的,时间复杂度 O(nlogn),但如果不是,比如每次分区都是不均等的,最坏情况时间复杂度就为 O(n^2)
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。
T(n) = T(n/10) + T(9*n/10) + n; n>1用快速排序可以以 O(n)的时间复杂度找到数组中第 K 大的元素,因为每次都会选中一个哨兵 pivot,利用好这个哨兵的下标位置,就能很容易找到第 K 大的元素
桶排序
线型排序算法
核心思想是将要排序的数据分到几个有序的桶里,每个桶里再单独进行排序,各自排序完后再取出组合,组成的序列就是有序的了
桶排序的时间复杂度 O(n)。如果要排序的数据有 n 个,我们把它们均匀地划分到 m 个桶内,每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序,时间复杂度为 O(k _ logk)。m 个桶排序的时间复杂度就是 O(m _ k * logk),因为 k=n/m,所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时,log(n/m) 就是一个非常小的常量,这个时候桶排序的时间复杂度接近 O(n)。
看起来很不错,但是桶排序对于数据的要求实际上是非常苛刻的
- 首先,数据要很容易划分成桶,并且桶与桶之间有着天然的大小顺序。这样每个桶排完序才能直接合并
- 数据在各个桶内的分布如果是均匀的,很好,但如果不均匀,极端情况下都分到一个桶里,那就变成 O(nlogn)
桶排序适合用在外部排序中
外部排序。数据都存储在外部磁盘中,很大,但是我们的内存有限,无法全部加载到内存中
比如 10G 的订单数据,但是我们只有 100mb 内存,需要加载进来按订单金额排序
我们可以获取订单金额的范围,比如是 1 元-10 万元,将其划分到 10 个桶里,第一个桶是 1-10000,第二个 10000-20000...如果理想的话,数据分布均匀,每个桶里就会有 10mb 左右的数据,逐个用快排排序,最后合并起来就是一份从小到大的订单数据
但是数据不可能那么均匀,我们可以针对数据量大的区间接着划分小区间,直到能读取到合适的数据量为止
计数排序
是桶排序的一种特殊情况,往桶里塞入相同的数据,这样就不需要桶内排序,直接合并就完事了,只涉及遍历扫描,时间复杂度 O(n)
计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合。而且,技术排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数(其实 js 用键值对就不存在这个问题)
基数排序
比如给手机号排序,可以从最后一位开始排序,时间复杂度 O(n)
如果是给英文单词排序,长度不一,但是可以通过补 0 来解决,因为 ASCII 码,所有字母都大于 0,补 0 不会影响原有得大小顺序。
技术排序对数据有要求,需要可以分割出独立的位来比较,而且位之间有递进的关系,如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序
排序优化
线性排序算法时间复杂度较低,适用场景特殊,通用的排序函数不能选择线型排序算法
快速排序较为适合,但是快速排序的最坏情况时间复杂度是 O(n^2),主要还是因为分区点选的不够合理,最理想的分区点是被分开的两个分区中,数据的数量差不多
有两个比较常用、简单的分区法
- 三数取中法。从区间的首尾中分别取出一个数,然后对比大小,取这 3 个数的中间值作为分区点,但是如果排序的数组比较大,那可能就要五数取中或者十数取中
- 随机法。随机选择一个元素作为分区点
在实际使用中,排序并不一定仅限于单一场景,通过针对不同情况灵活运用才能让执行效率更高。比如 qsort 函数
qsort 会优先使用归并排序,因为数据量小的时候,归并排序更快,空间换时间,但是数据量大的时候,会改用快速排序(三数取中法)。当元素个数小于等于 4 时,qsort 使用插入排序
查找算法
二分查找
复杂度 O(logn),效率极高,但是有局限性
- 二分查找依赖顺序表结构数组,其他的数据结构不适用
- 数组必须有序。二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中,针对动态变化的数据集合,二分查找将不再适用
- 如果数据量很小,没有必要用二分查找,顺序遍历即可。但是如果数据项都是长度超过 300 的字符串就要使用二分,因为 300 长度字符串的大小对比很耗时
- 数据量太大也不适合二分。因为二分查找要求数组,而数组是内存空间连续的数据结构,如果数据量太大,对内存空间的要求太苛刻。(JS 的数组由于是对象模拟出来的,不必在意这个)
二分查找的变形问题
const x = [1, 2, 3, 46, 46, 46, 90];
const bSearch = (array, n, value) => {
let low = 0;
let high = n - 1;
while (low <= high) {
let mid = low + ((high - low) >> 1);
if (array[mid] >= value) {
high = mid - 1;
} else {
low = mid + 1;
}
}
if (low < n && array[low] === value) return low;
else return -1;
};查找第一个值等于给定值的元素
分两种情况,算上右侧边界,需要定 right=nums.length-1,否则不用减 1
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function (nums, target) {
let left = 0;
let right = nums.length - 1;
while (left <= right) {
let middle = left + (right - left) / 2;
if (nums[middle] < target) {
left = middle + 1;
} else if (nums[middle] > target) {
right = middle - 1;
} else {
return middle;
}
}
return -1;
};移除元素
这种题目的关键在于,数组元素在内存中的地址是连续的,不能单独删除某个元素,,只能覆盖 可以采用双层 for 循环,一层遍历数组元素,一层在发现需要移除元素后,将数组集体向前移动一位,但是时间复杂度为 O(n^2),因此不推荐 使用双指针法,只需要一层 for 循环,遇到目标元素时,会区分出快慢指针,从而移动元素位置,时间复杂度为 O(n)
/**
* @param {number[]} nums
* @param {number} val
* @return {number}
*/
var removeElement = function (nums, val) {
let slowIndex = 0;
for (let i = 0; i < nums.length; i++) {
if (nums[i] !== val) {
nums[slowIndex++] = nums[i];
}
}
return slowIndex;
};滑动窗口
像一个窗口一样,每当和大于目标值时,就移动左右窗口,这道题有个坑,就是每当和大于目标值时,计算子串长度不需要加 1,因为在这一步里必然会减去左侧的一个值,必然需要减去 1
/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function (target, nums) {
let subLength = 0;
let left = 0,
right = 0;
let sum = 0;
// 给一个不可能的值,没有改变就说明不存在目标子串
let result = nums.length + 1;
for (let i = 0; i < nums.length; i++) {
sum += nums[right++];
while (sum >= target) {
subLength = right - left;
result = result < subLength ? result : subLength;
sum -= nums[left++];
}
}
// 可能存在全部相加也不大于等于目标值的情况
return result <= nums.length ? result : 0;
};有序数组的平方排序
这类题可以用双指针法,直接将时间复杂度降到了 O(n)
/**
* @param {number[]} nums
* @return {number[]}
*/
var sortedSquares = function (nums) {
let k = nums.length - 1;
let i = 0,
j = nums.length - 1;
let result = [];
while (i <= j) {
if (nums[i] * nums[i] < nums[j] * nums[j]) {
result[k--] = nums[j] * nums[j];
j--;
} else {
result[k--] = nums[i] * nums[i];
i++;
}
}
return result;
};